作成したモデルが良いものであるか、そうでないかを判断するにはどうすればよいでしょうか。よく使われる手法としては、交差検証(分割交差検証、n-fold cross-validation)が行われます。
n-fold cross-validation
これは、クラスとベクトルが全て分かっているデータを用意したときに、そのデータをnグループに分割し、n-1のグループ(訓練用のグループ)のデータを使ってモデルを作成し、残りの1グループ(テスト用のグループ)でどれだけ正解に近いクラス分けができるかを数値的に検証するものです。これを、テスト用のグループを変えることによってn通り検証し、数値結果を平均して、全体のモデルの良さを計算するのが、分割交差検証です。
数値的な評価
正解のクラスというのが既に分かっていて、それとは別にSVMによってクラスに属するか属さないかという出力が得られます。この2つの組み合わせは、以下のマトリクスに分けることが出来ます。
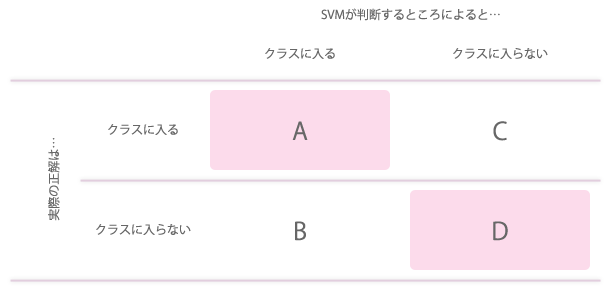
つまり、文にすれば下記の4通りがあるということです。
- 正解データではクラスに属すものであって、SVMもクラスに属すものと判定した(上の表のAのもの。正しい判断をしている)
- 正解データではクラスに属すものではないのに、SVMはクラスに属すものと判定した(上の表のBのもの。間違った判断をしている)
- 正解データではクラスに属すものであるのに、SVMはクラスに属さないものと判定した(上の表のCのもの。間違った判断をしている)
- 正解データではクラスに属さないものあって、SVMもクラスに属さないものと判定した(上の表のDのもの。正しい判断をしている…かもしれない)
正解っぽいのは、AとDに含まれるものです。TinySVMでは、テスト用のデータのうち、AかDに属したものの割合を、Accuracyとして計算しています。
![]()
しかし、あまりこのAccuracyが重要視されることは、著者の個人的な印象ではあまり無いように思えます。というのも、例えばテストデータが1000あって、そのうちクラスに属すものが10程度しか無かった場合、全てをクラスに属さないと判定すれば、それだけでAccuracyが99%となるからです。
それよりも重要な事は、クラスに属すべきものが、正しくクラスに属すと判定されることです。つまり上の表で言うとAの部分にどれだけ入ったかが重要です。ただし、Aに属すデータの数は、テストするデータのサイズにもよりますし、クラスに含まれるデータの数にもよります。従って割合で示す必要があるのですが、この割合を計算する方法が、2つあります。
一つは、精度(Precision, 適合率)であり、これは、SVMがクラスに属すと判断したもののうち、本当の正解でもクラスに属すものであった割合を言います。
![]()
もう一つは、再現率(Recall)であり、これは、本当の正解でクラスに属すものであったもののうち、どれだけSVMがクラスに属すと判断したかの割合を言います。
![]()
これら2つは基本的にトレードオフの関係にあるものです。つまり、SVMが全てのデータに対してクラスに属すと判定すれば、再現率は1となります。しかし、精度は相当低いものとなるでしょう。逆に、クラスに属すと判断するハードルを相当上げれば、精度は上がるでしょうけれど、再現率は下がりそうですね。
この2つの値が、うまく調和するように入力データやSVMを調整する必要がありそうです。
次回は、SVMにオリジナルのデータを入力して観察してみたいと思います。